Power of Compounding!
It’s not an exaggeration to call compounding the 8th wonder of the world. The path to immense wealth lies in letting your money grow. Regularly withdrawing returns is akin to a fixed-income job. Investors employ various methods to achieve compounded returns. While bank fixed deposits offer safety, their interest rates are meager. It could take generations to witness substantial growth. Mutual funds SIPs and equity investments offer superior ROI.
Also Read: Unlocking Stock Market Profits: Margin Trading Explained
Exponentially increase investments
In this article, we will delve into how compounding can exponentially increase investments. For beginners, compounding involves reinvesting returns in the same instrument, resulting in ‘Compound Interest.’ For example, investing 100,000 Rupees at a 10% annual compound interest would yield the following:
| Year | Principal | Interest (10%) |
|---|---|---|
| 1 | 100,000 | 10,000 |
| 2 | 110,000 | 11,000 |
| 3 | 121,000 | 12,100 |
| 4 | 122,100 | 12,210 |
| 5 | 146,410 | 14,641 |
| 6 | 161,051 | 16,105.1 |
| 7 | 177,156.1 | 17,715.61 |
| 8 | 194,871.7 | 19,487.17 |
Observe how the capital almost doubled in 8 years due to compounding. Compounding doesn’t have to occur annually; it can be monthly, weekly, or even daily, with shorter intervals showcasing its true power. The graphical illustration below illustrates compounding’s impact at varying interest rates:

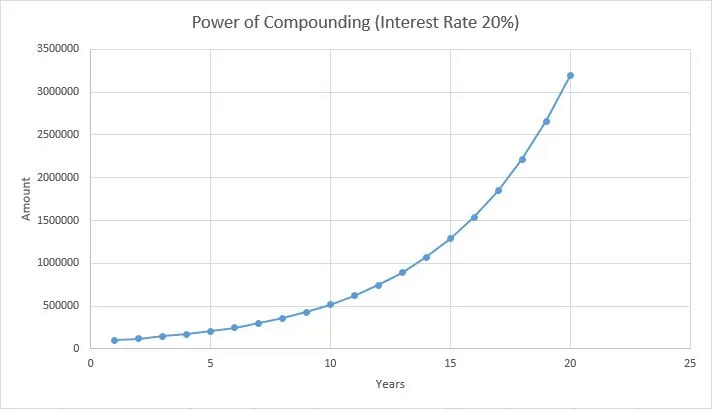
Also Read: 5 Pitfalls to Avoid: The Road to Profitable Stock Market Trading
Formula
Traders can significantly benefit from compounding by reinvesting returns into their portfolios. A sound trading system can yield over 20% annual returns. Given time to grow, this can multiply your wealth rapidly. However, effective risk management and position sizing are essential for long-term wealth growth.
The following formula calculates the total amount through compounding:
- Where:
- A = Final Amount Received
- P = Principal Amount (Initial Investment)
- r = Annual nominal interest rate (as a decimal, e.g., 10% as 0.1)
- n = Number of times the interest is compounded per year (e.g., 12 for monthly compounding, 2 for semi-annual, and 4 for quarterly)
- t = Number of years
Download our Excel sheet for the calculations:
Also Read: Trading Software in India: Alternatives to Amibroker




5 Comments